java二维数组打印杨辉三角详解版

0.观察规律

首先我们需要知道什么是杨辉三角。

杨辉三角，是二项式系数在三角形中的一种几何排列，

中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。-来源百度百科

下面两张图分别是在正常情况下和我们要编写的程序中的杨辉三角的形式。后续我们以第二张图为准编写程序。

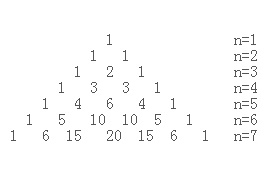
观察上图可见（如果把i看成行数，j看成列数），则有以下规律：

1. 第一行有1个元素，第n行有n个元素
2. 每一行的第一个元素和最后一个元素都是1
3. 从第三行开始，对于非第一个元素和最后一个元素的元素值arr[i][j] = arr[i-1][j]+arr[i-1][j-1];

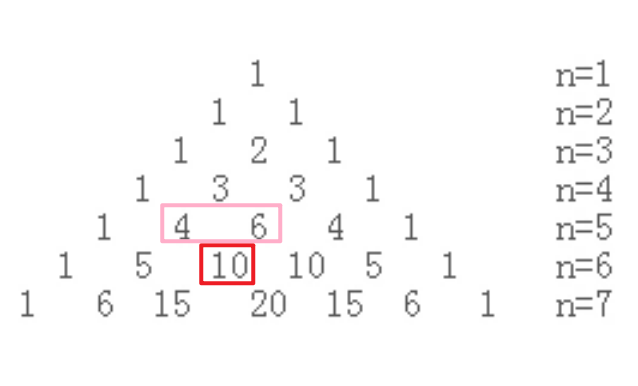
画图解释arr[i][j] = arr[i-1][j]+arr[i-1][j-1]，看图可知就是上一行同一列的值加上前一列的值。

如果换成正常三角形的话，即为当前数字的上一行两边的值相加。

1.编写程序

思路有了，我们开始编写程序。

首先附上完整代码：

public class Main {

	public static void main(String[] args) {

		int[][] yangHui = new int[10][];//定义二维数组
		for(int i = 0;i< yangHui.length;i++) {//循环一维数组长度
			yangHui[i] = new int[i+1];//初始化二维数组
			//循环二维数组长度
			for(int j = 0;j < yangHui[i].length;j++) {
				//判断是否为第一行或者最后一行
				if(j == 0 || j == yangHui[i].length - 1) {
					yangHui[i][j] = 1;
				}else {
					//不是第一行或最后一行则执行规律
					yangHui[i][j] = yangHui[i-1][j] + yangHui[i-1][j-1];
				}
			}
		}
		//打印输出
		for(int i =0;i<yangHui.length;i++) {
			for(int j=0;j<yangHui[i].length;j++) {
				System.out.print(yangHui[i][j]+" ");
			}
			System.out.println();
		}
		
	}
}

下面是代码详解：

首先对二维数组进行定义，因为我们要打印的是10行的杨辉三角，所以数组的行为10，因为列数不确定所以进行动态初始化。可以将10换成一个变量，那么我们就得到了一个通用的杨辉三角打印程序。

int[][] yangHui = new int[10][];//定义二维数组

下面我们进行循环操作，for(int i = 0;i< yangHui.length;i++)第一个外层循环，意义是遍历二维数组中的每一行，因为i从0开始，到yangHui.length - 1因为是小于，所以为减一。

因为我们在定义二维数组时因为列数不固定所以决定对列数进行动态初始化。这里我们就可以运用上前面我们总结出的第一条规律第i行有i个元素，因为i为数组下标是行数的减一，所以我们进行i+1的操作，然后进行初始化。

yangHui[i] = new int[i+1];//初始化二维数组

列初始化完成之后，我们再对每一行中的各个元素（也就是刚刚我们初始化的列元素）进行for循环遍历也就是在刚刚外层循环中的内层小循环。

for(int j = 0;j < yangHui[i].length;j++)

然后我们根据总结出的规律进行判断，

是不是每行的第一个元素或者是最后一个元素，如果是则赋1，如果不是则按照规律进行赋值，如下：

//判断是否为第一行或者最后一行
if(j == 0 || j == yangHui[i].length - 1) {
	yangHui[i][j] = 1;
}else {
	//不是第一行或最后一行则执行规律
	yangHui[i][j] = yangHui[i-1][j] + yangHui[i-1][j-1];
}

整个赋值操作就结束了，下面进行打印即可。

完整代码请看讲解开始部分，如果觉得有用不妨留个言，还想看什么文章？